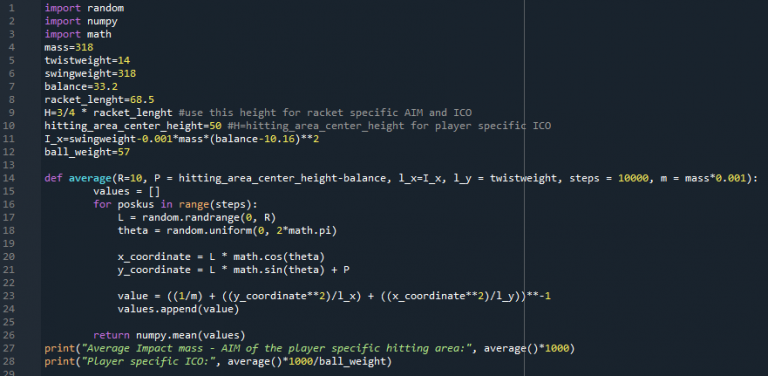
Effective Mass -> Average Impact Mass or. AIM
Effective Mass or Racket Hittingweight like Tennis Warehouse University calls it.
In this chapter, we will take a closer look at the ball-to-racket interaction and what affects the energy return and transfer between the ball and the racket. The impact between the ball and the racket, or it’s string bed, and the location of the impact point, will determine the control we have over the ball and the velocity it travels with, after it leaves the string bed.
To quantify the racket’s ability to give a player the desired outcome after the ball leaves the string bed, I defined the Average Impact Mass – AIM. It should be noted that there are other factors, like stiffness, string pattern etc, but they do not have an effect on racket specifications like swingweight, twistweight, mas, balance, MGR/I and so on. Through my research, testing and experience, I found out that the most important parameters are average effective mass and MGR/I.
The average impact mass is the average effective mass of the specific area on the racket string bed at contact. It reflects how fast we can swing the racket, while providing adequate control and energy transfer to the ball, despite not hitting the ball right in the sweet spot. In other terms, it means we can swing the racket faster, while still taking less risk of losing control and power because the impact point was away from the optimal point of contact.
If you are not interested in the derivation of the equations, you can skip straight to the calculator At the bottom of the page. First we need to define the effective mass of the racket, which can be calculated for any point on the string bed, by using these known parameters:
- Mass,
- Swingweight,
- Balance,
- Twistweight,
- coordinates of the point of contact (r, b).
Let’s first define some relations and equations:
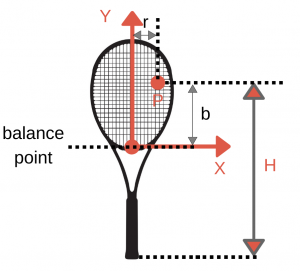
We can write down:
\(F=m_{e}\cdot a=m_{e}\dfrac{dv}{dt}\)
\(F=m\dfrac{dv_{cm}}{dt}\)
These are the basic Newtons equations written for a force acting on the racket at a specific point where the effective mass is Me, resulting in acceleration a. The same goes for the center of mass (cm), where effective mass is the actual mass of the racket m. We can continue by writing the relation between the speed of the impact point (v) and the velocity of the center of mass (vcm), by using the angular speed:
\( v=v_{cm}+b\omega _{x}+r\omega_{y} \)
By differentiating the eqation over time, we get:
\(\dfrac{dv}{dt}=\dfrac{dv_{cm}}{dt}+b\dfrac{d\omega_{x}}{dt}+r\dfrac{d\omega _{y}}{dt}\)
We can write down the equation for torque around both axis, with force F on both levers b and r:
\(Fb=I_{x}\dfrac{d\omega _{x}}{dt}\)
\(Fr=I_{y}\dfrac{d\omega _{y}}{dt}\)
Both moments of inertia, Ix and Iy, around axis x and y, are actually what we know as recoilweigh and twistweight. By rearranging the equations we get:
\(\dfrac{F}{m_{e}}=\dfrac{F}{m}+\dfrac{Fb^{2}}{I_{x}}+\dfrac{Fr^{2}}{I_{y}}\)
Dividing everything by F and expressing effective mass we get the equation for effective mass at any point on the string bed:
\({m_{e}}=\left( \dfrac{1}{m}+\dfrac{b^{2}}{I_{x}}+\dfrac{r^{2}}{I_{y}}\right) ^{-1}\)
You can calculate the effective mass for your racket for any point of contact with the calculator at the bottom of this page.
This information is useful, but it does not give us any insight into racket’s characteristics in general. That is why I defined the Average Impact Mass, which is an average of the effective mass on a specific hitting area on the string bed. It reflects how fast we can swing the racket, while providing adequate control and energy transfer to the ball, despite not hitting the ball right in the sweet spot. In other terms, it means we can swing the racket faster, while still taking less risk of losing control and power because the impact point was away from the optimal point of contact.
For this reason we need to determine the average effective mass on the hitting area, by integrating the effective mass equation on the interval of the hitting area. The hitting area is different for every player, as we don’t all hit the ball in the same sport. For example, some players might hit the ball higher on the string bed, which enables a player to hit more topspin, because the velocity of the racket is higher there, but effective mass is lower. That’s why I differentiate from player-racket AIM and racket specific AIM:
Personal AIM:
The center of the hitting area has to be determined experimentally, by observing the impact point pattern. We can do this with cameras or by examining the stringbed and determining the area where strings are notching more. A more reliable method is to color the string bed and play, while the paint wears off. This will give us a good idea of our hitting zone location.
Racket specific AIM:
The center of the string bed is determined to be ¼ of the length of the racket away from the top of the racket.
Let’s take a look at how we can determine the average impact mass (AIM) for given racket specifications. We need to determine the average effective mass over the area, where we hit the ball most of the time. As the industry standard I defined an area as a circle with the center (P) at height (H) of ¾ (or custom height for player specific) of the racket length and a radius (R) of 10 cm. Let’s take a look at how the area is defined:
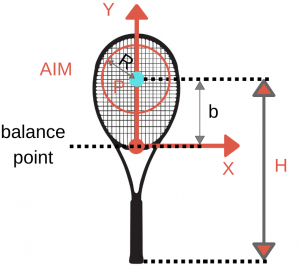
To get the average impact mass, we need to calculate it in every point in the area and then divide it by the number of points. We can also do this, by solving a definite integral:
\(AIM = \overline{m}_{e}=\overline{f\left( t,b\right) }=\iint _{D} f\left( r,b\right) drdb\)
\(\overline{m}_{e}=\iint _{D}\left( \dfrac{1}{m}+\dfrac{b^{2}}{I_{x}}+\dfrac{t^{2}}{I_{y}}\right) ^{-1}drdb\)
We need to translate the integral to polar coordinates:
\(\begin{aligned}\int ^{R}_{0}\left[ L\int ^{2\pi }_{0}\left( \dfrac{1}{m}+\dfrac{\left( L\cdot \sin \left(\varphi \right) +P\right) ^{2}}{I_{x}}+\dfrac{L^{2}\cdot \cos ^{2}\left( \varphi \right) }{I_{y}}\right) \right] d^{\varphi }dL\\ .\end{aligned} \)
Unfortunately, after some effort, we quickly realize that the integral cannot be solved uniformly. We need to simulate the calculation for as many points as possible. I made a good approximation in the Customization tools Excel file, which you can get by subscribing to my Customization Tools.
For more tech-savvy people, I wrote a Python code, to simulate the AIM more accurately. You can get it here on GitHub.