Mass and balance -> MR^2
Mass and balance are the basic parameteres of each racket that everyone thinks of, but not the only ones, nor the most important. Still, these are the parameters that we associate with a tennis racket the most because they are physical concepts that are the easiest to wrap our minds around (unlike swingweight and MGR/I). The most common description of any object is it’s weight and length/height. But if we want to determine the center of mass or balance of an inhomogeneous object we have to introduce the weight distribution relative to a point in space. In the case of a racket, we take the start of the handle (also called butt cap) as the reference point. Next, we consider the racket as a system of infinitely small particles. Let’s define the axes of the racket on the picture below:
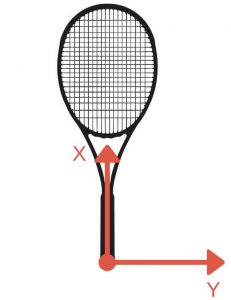
For now, we only consider the X-axis. We will consider the weight distribution along the Y-axis in the twistweight chapter. Each particle is at distance x (the balance point of each particle) from the butt cap and has a mass of m. To determine the balance point of the racket, we can write down the following equation:
\(x_{B,i}=\dfrac {\sum ^{n}_{i=1}x_{i}\cdot m_{i}}{\sum ^{n}_{i=1}m_{i}}\)
(1)
In practice, when modifying rackets we would of course measure the balance point by simply balancing the racket on a balance board or an edge of a table etc., and measure the distance. Check the chapter swingweight for an ideao of how to measure balance.
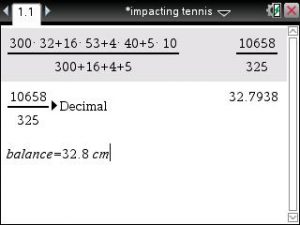
The equation (1) becomes useful when we know the weight and balance of the racket, and we want to calculate the effects of adding weight at different locations. For example, we have a racket that weights 300 g with a balance point of 32 cm. This is an unstrung racket, with no overgrip and dampener. To get the final specifications we need to consider a 4 component system with corresponding masses and centers of mass (given parameters serve as an example):
– Racket (m=300 g, x=32 cm),
– Strings (m=16 g, x=53 cm),
– Dampener (m=4 g, x=40 cm),
– Overgrip (m=5 g, x=10 cm).
Using the above equation (1) we get the new balance point of 32,8 cm as shown on the picture below.
When using this equation (1) it’s important to know when the added weight is a homogenous mass system, meaning that the center of mass is also the geometrical center.
Homogenous mass system
The mass is spread evenly along the considered vector (axis) in space. Meaning we can treat its geometry center as the center of mass. For example, adding the overgrip on the handle will add about 5 grams, and will spread from the butt cap to about 20 cm up the handle. The overgrip will take a shape of a cylinder and a geometrical center of a 20 cm long cylinder along the handle is at 10 cm.
Inhomogenous mass system
The mass is spread unevenly along the considered vector (axis) in space. An example of such system is a racket. If you divide the racket by 10 sections of equal length along its centerline and measure the mass of each piece, they won’t be the same. For example, there will be more mass in the head, where there are strings, more material to form the hoop etc. If we want to get in some serious detail, we should also consider added lead tape as inhomogenous, especially when adding it to the top of the racket (so-called 11, 12 and 1 o’clock locations), the mass will not be evenly distributed along the x-axis of the racket, but along the radius of the racket head curvature.
Using the above equation (1) we get the new balance point of 32,8 cm. Now let’s say you want a balance of 33 cm, and you want to achieve this by using lead tape. You don’t want to polarize the racket too much, and maybe you also want to increase the twistweight, so you want to add the weight on the sides of the hoop (so-called 3 and 9 locations). Now we can use the equation to determine the amount of lead we need to add to achieve the desired balance. The known and unknown values are:
– Racket (m=325 g, x=32,8 cm),
– Lead tape (m=?, x=53 cm),
– Desired Racket (m=? g, x=33 cm).
By extracting the unknown variable we can determine the mass we need to add.

Like shown above we need to add 3, 25 g and the final specifications are 33 cm and 328,25 g. Note that the added weight at this location will also increase the swingweight. It’s worth mentioning that in practice it makes no sense to use more than 0,1 accuracy, so let’s round that to 3, 3 g and 328, 3 g.
In this example, we only considered mass and balance but didn’t give much attention to the mentioned swingweight, twistweight and polarization. You can learn more about these in other chapters, here we will only focus on mass and balance.
I have also created spreadsheets for customization and more, that I use for my work as shown on the picture below. I also share this and more with my supporters.
Head light and head heavy
By definition, a racket is head light when the balance point is between the middle of the racket (geo. center) and the butt cap. Vice versa, a head heavy racket will have the balance point above the middle. For a standard length (27 inches/68, 6 cm) the middle would then be 34, 4 cm. So points head light/heavy is the difference between the geometric center and the mass center. I like to use and think in terms of balance point distance from the butt cap. On the table below I have gathered the conversions.
| Balance[cm] | Points HL/HH | |
| 38,14 | 12 | Head Heavy |
| 37,82 | 11 | Head Heavy |
| 37,50 | 10 | Head Heavy |
| 37,18 | 9 | Head Heavy |
| 36,86 | 8 | Head Heavy |
| 36,54 | 7 | Head Heavy |
| 36,22 | 6 | Head Heavy |
| 35,90 | 5 | Head Heavy |
| 35,58 | 4 | Head Heavy |
| 35,26 | 3 | Head Heavy |
| 34,94 | 2 | Head Heavy |
| 34,62 | 1 | Head Heavy |
| 34,30 | 0 | Even |
| 33,98 | 1 | Head Light |
| 33,66 | 2 | Head Light |
| 33,35 | 3 | Head Light |
| 33,03 | 4 | Head Light |
| 32,71 | 5 | Head Light |
| 32,39 | 6 | Head Light |
| 32,08 | 7 | Head Light |
| 31,76 | 8 | Head Light |
| 31,44 | 9 | Head Light |
| 31,12 | 10 | Head Light |
| 30,81 | 11 | Head Light |
| 30,49 | 12 | Head Light |
But for me, when I think in terms of head light and head heavy, a head light racket is anything with a balance below 32, 5 cm, and head heavy with 32,5 cm because my model of thinking is built around a range of racket balances that I found useful.
The essence of balance and mass
It is important to understand that two rackets of the same model, that have the same weight and balance, can have very different playing characteristics. Only considering the static weight and balance, I have condensed some generalizations through my rigorous testing and observation:
- First one should be obvious, a heavier racket can generate more ball speed/power, provided we can swing it with the same swing speed through the contact point.
- For any serious player, the balance should be around or bellow even (34,3 cm) and above 31 cm.
- Generally, you can compensate for the lack of weight with a more »head heavy« racket and vice versa.
- For a great two-handed backhand, you need a balance of 32,5 cm or more, but than the balance starts causing problems on the forehand side. This is for a simple reason, that we hold the racket higher up the handle with both hands and thus shift the pivot point higher, lowering the effective racket balance and dynamic weight (swingweight).
- Having a one-handed backhand makes it easier to optimize the mass and balance for both wings because the pivot point is the same with both strokes. Pro players with one-handed backhand and more »head light« rackets (Federer, Wawrinka, Shapovalov) can usually hit exceptional shots from both sides. And then there is someone like Grigor Dimitrov, who is the complete opposite of this theory. He has a more »head heavy« setup, and a one-handed He compensates heavily with his athleticism and doesn’t get any help on his shots from the racket, and that’s why I believe with this kind of setup, he will never be on the top of the men’s game.
- More »head light« rackets are better for the serve and just about any shot with 1 hand,
- MR^2 is useful, to determine the limitations of the player or. how much weight leveraged by distance R can the player handle. This is based on players strenght, stamina and what the joints can handle.
These points are oversimplified for just using mass and balance. To see the bigger picture we need to consider much much more. Using this theory we should also conclude that Nadal has a bad forehand (which I don’t think is the case), because his setup is more »head heavy«, which in a sense is true, as his forehand is only good when he has a lot of time to hit the ball, and why players are targeting the forehand with the serve on faster surfaces. Also, let’s not forget how much energy he has to exort for every forehand that he hits. Again an example of how you racket setup effects your style of play and stroke technique.
To understand how mass effects power and ball speed, let’s take a look at the first point I made: »heavier racket can generate more ball speed/power«. Consider the collision of the ball and the racket in 1 dimension. When modelling the collision now, we can only use the momentum equations and the law of conservation of momentum:
\(m_{1}u_{1}+m_{2}u_{2}=m_{1}v_{1}+m_{2}v_{2}\)
(2)
We can see that the only factors that impact ball speed after collision (velocities v) are the starting velocities (velocities u) and mass of the racket and ball respectively. Of course the actual model should be a multidimensional (3D) and the swing path of the racket and the arm is a multi pendulum model. Here we can no longer describe the racket only as a colliding mass, but we need to introduce some new parameters which I like to call dynamic weight.
Static and dynamic weight
I use the terms dynamic and static weigh, as mentioned earlier. When we put the racket on a scale, the mass that we measure is static weight. In contrast, the dynamic weight cannot be measured on a scale, and can only be determined when we put an object (racket) in motion and introduce the momentum equations. Many different parameters can be understood under this term, but in tennis, we mainly consider kinetic energy and angular momentum. Some parameters that are »influenced« by dynamic weight are swingweight, twistweight and MGR/I. Using the equation in this chapter to calculate the final mass and balance, we consider the racket to be homogenous. But when dealing with momentum equations, 2 rackets with the same balance and mass can have different moments of inertia, that’s because their weight distribution is different. To incorporate this in tennis we use the mentioned swingweight, twistweight and MGR/I.
MR^2
The most basic dynamic weight is the moment of inertia of the center of mass. If we treat the racket as a rod with all mass M concentrated in the balance point R, we can calculate the moment of inertia of the racket around the axis X at the bottom of the handle:
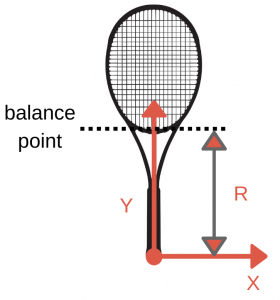
We calculate it by using a simple equation:
\(I_{x}=M\cdot R^{2}\)
MR^2 is useful, to determine the limitations of the player or. how much weight leveraged by distance R can the player handle. This is based on players strenght, stamina and what the joints can handle.