Swingweight

As we saw in chapter mass and balance, if we only consider the collision of the ball and the racket in 1 dimension, we are fine only using the momentum equations and the law of conservation of momentum. We determined that the only factors that impact ball speed after collision are the starting velocities and mass of the racket and ball respectively. Of course the actual model should be a multidimensional (3D) and the swing path of the racket and the arm is a multi pendulum model. Here we can no longer describe the racket only as a colliding mass, but we need to introduce some new parameters which I like to call dynamic weight.

Swingweight is a dynamic parameter, which can be defined as the moment of inertia I, also known as the rotational inertia. Rotational inertia of a rigid body (racket) is used to determine how much torque is needed to achieve the desired angular acceleration about the rotational axis. Let’s take a look at the axes of the racket again.

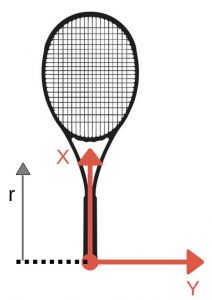
The moment of inertia of a rigid composite system is the sum of the moments of inertia of its component subsystems that are at the distance r from the same axis. Now we can write down the general equation for the moment of inertia.

\(I_{p}=\iiint \rho _{\left( x,y,z\right) }\cdot \left| \left| r\right| \right| ^{2}dxdydz\)

(1)

There are 2 parts of the equation. The first is the integration of the density over the whole volume of the racket, which represents mass, and the second part is the radius or distance r of the mass particle from the rotational axis. For the purpose of racket modification, we don’t need the equation in this form, and we can write down a discretized form.

\(I _{p y}=\sum ^{n}_{i=1}\left( m_{i}\left( r_{i,y}\right) ^{2}\right)\)

(2)

Now we get the expression for the moment of inertia I around the axis Y, as the sum of moments of inertia of all the mass components. In practice, those mass components can be strips of lead, vibration dampener, strings etc. that are at distance r from the Y-axis.

But in tennis, we use swingweight, which is just a moment of inertia about the parallel axis to the Y-axis, as shown in the picture below.

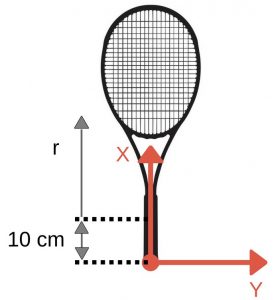
We can see that the parallel axis is 10 cm from the axis Y. This is just the industry standard or I should say an arrangement. The axis is set at a distance of 10 cm because of the way we hold the racket, and the pivot point of the racket is not about Y-axis. Of course, this depends on the grip style we use, how big are our hands etc., but we need some common grounds to characterize rackets. If you know the moment of inertia about any given axis, you can calculate it about any other parallel axis. The final expression for swingweight is as follows.

\(SW=\sum ^{n}_{i=1}\left( m_{i}\left( x_{B,i}-10 cm\right) ^{2}\right)\)

(3)

Racket as a physical pendulum

Physical pendulum is any swinging rigid body free to rotate about a fixed horizontal axis. We need to consider the racket as a physical pendulum in order to determine it’s swingweight. The equation below describes the basic physical pendulum.

\(T_{0}=2\pi \sqrt {\dfrac {I_{p}}{mgR}}\)

(4)

In the equation, I is the moment of inertia of the pendulum about the pivot point, m is the mass of the pendulum, R is the distance between the pivot point and the centre of mass, T is the period of oscillation (swing time) and g is acceleration of gravity. By rearranging the terms we can get an expression for the moment of inertia

\(I_{p}=\dfrac {m\cdot g\cdot R\cdot T^{2}_{0}}{4\cdot \pi ^{2}}\)

(4)

Further, we can derive the equation for the swingweight using the racket balance x and the distance r (distance of the pivot point).

\(SW=m\left( \dfrac {rT^{2}_{0}g}{4\pi ^{2}}-r^{2}+\left( x_{B}-10cm\right)^2 \right)\)

(5)

We can use this expression to calculate swingweight by measuring all the parameters. 

Usually, there are no units given when listing swingweight, just a number of about 200-400, which is the industry standard and is used so that the SW is roughly comparable to the mass of the racket. The units of SW are actually kg*cm2 and it’s what you should use in the equations to get comparable results in that range.

More on this and how to measure swingweight in the DIY chapter and in the video below, where I demonstrate how to use this formula.

The spreadsheets used in the video and as shown on the picture bellow, are part of my calculation tools that I use for my work. I have them available for my supporters.

Support me

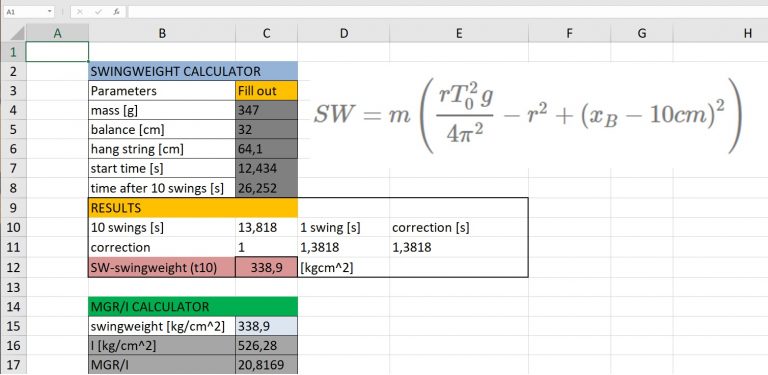
Calculating swingweight

Now let’s take a look at how mass added at different locations affects the swingweight. Let’s continue with the example from the chapter mass and balance:

 

  • Racket (m=300 g, x=32 cm),
  • Strings (m=16 g, x=53 cm),
  • Dampener (m=4 g, x=40 cm),
  • Overgrip (m=5 g, x=10 cm),
  • Lead tape (m=3,3 g, x=53 cm).

 

We have determined that the final specifications are 33 cm balance and a mass of 328, 3 g. But what about swingweight? For the sake of the example, let’s say that we know the SW of an unstrung racket, which is 290. This is not the information that manufacturers or retailers usually give about the racket. They give the number for SW for a strung racket, or they don’t specify swingweight at all. First of all, the weight, balance and swingweight between the same model of rackets vary, because of manufacturing tolerances. From my own experiences by weighting rackets, the tolerances can be up to 10 g for mass alone. As shown on the picture below they even print the tolerances on the racket.

The +- 7 g and +- 7 mm may not seem like much, but try playing with 2 rackets in the opposite tails of that distribution and you’ll know what I’m talking about. And this is just the weight and balance, things get much more complicated when we try to figure out where the missing or the extra 7 g are located. From this perspective, I believe it’s correct to not list the swingweight, but when they do it, I think it’s a mistake to list a strung racket swingweight because the weight of the strings you put in a racket also vary up to 5 g or even more. Furthermore, the numbers they list for a racket are an average of the sample size that they measure. If you want any kind of consistent specifications among your rackets or you want to change some parameters for a specific purpose, it’s essential to know and to calculate mass, balance, swingweight, MGR/I etc. of every racket in your bag and not assume that the racket has the specifications of the advertised average. Because of this variations, we match rackets to the desired specifications, by adding weight or sometimes removing it if possible.

Let’s get back to our example, and take a look at how to calculate the effect of added weight on swingweight. We know the SW of an unstrung racket to be 290. Now we add the strings:

  • Strings (m=16 g = 0,016 kg, x=53 cm)

To get the total SW of the strung racket we just use the parallel axis theorem and add the SW of the strings to the SW of the racket.

Using the equation (3) and mass in kilograms, we can calculate the SW of the strings as shown in the picture below.

I selected the strings for the example because while doing modifications it’s very important to plan ahead and know how much the strings add up to swingweight and mass.

 

Next, let’s take a look at lead tape (1 g) at the top of the hoop or so-called 12 o’clock position:

 

  • Lead tape (m=1 g = 0,001 kg, x=68 cm)

As shown in the picture above 1 g of lead at 12 o’clock is approximately 3, 4 SW. Knowing this is useful for a quick approximation of the SW increase. For more information on the weight of different string check the strings section.

 

Now let’s suppose we add 5 grams to the handle, more specifically under the grip at a distance of 5 cm from the butt cap and 15 cm from the butt cap:

 

  • Lead tape (m=1 g = 0,001 kg, x=5 cm)
  • Lead tape (m=1 g = 0,001 kg, x=15 cm)

 

As seen in the picture above, 5 grams at both locations add the same amount of SW, which technically is correct, if SW was just the moment of inertia, because they both have the same distance from the axis of rotation (10 cm from the butt cap). But generally, anything below the distance of 10 cm should not be included in the swingweight calculations. Even any mass on the handle has a very low impact on the swingweight because the distance in the equation is squared. Having more mass on the opposite side of the rotational axis has an impact on the recoil weight but not on the swingweight, but more on that in the recoilweight section.

How swingweight impacts stroke mechanics

Again I have condensed some generalizations on how the swingweight impacts the stroke mechanics and one’s game in general:

 

  1. High swingweight smoothes out the strokes and it makes almost impossible to just arm the ball with bad technique. That is because the racket has a higher moment of inertia and you have to generate more momentum with your hand to get it moving and small deviations of your hand movement and muscle action don’t affect the racket head position and path so much.
  2. Derived from the first point this translates to less maneuvrability and longer reaction times for volleys etc.
  3. Higher swingweight usually means lover MGR/I and that gives you the feeling that you are dragging the racket through the contact, and not pushing it. It gives you the feel of carving around the ball and giving you more control.
  4. More control and consistency also comes from the fact that with a higher swingweight you can swing at lover swing speed to get the same amount of power and spin.
  5. High swingweight also means you need longer strokes to accelerate the racquet. Think about Rafael Nadal and Alexander Zverev (Novak Djokovic is also here but not so extreme). They both have hight swing weight and low MGR/I, and they have long strokes, especially on the forehand side, and they play with incredible control and consistency. On the other side of the spectrum is, for example, Nick Kyrgios. Low swingweight, hight MGR/I, short strokes, incredible racquet head acceleration but a lack of consistency, because when he get’s tight, the slightest deviations in his stroke mechanics cause a much bigger change in the racquet head position at contact. On the other hand, Nadal and Zverev when they get tight their only job is to get the racket through the contact and the ball goes in. They spend much more energy doing that, but they can go in the »lockdown« mode and not miss.
  6. I generally advocate that players use as high of a swingweight they can play with, but without mistiming the ball when the matches get longer. It’s important to know your limits because a higher swingweight won’t be beneficial if it tires you or you can’t accelerate the racket enough before the contact.
  7. Higher swingweight is less forgiving and requires you to have better footwork, because of the longer strokes. Your positioning has to be better because you can’t make quick adjustments to your swing path.
  8. Higher swingweight can mean more spin (again if you can swing it). The racket has more angular momentum during the contact consequently more kinetic energy in the vertical direction, which means strings can move more and snap back, and impart more spin on the ball. Also, more angular momentum at impact means less deformation of the racket and more energy can be transferred to the ball (rotational and kinetic energy).
  9. Rackets with higher swingweight have a higher ceiling in a perfect world. Humans are not perfect machines in a perfect world, so we need to compromise and making compromises is the real artistry of racket modifications. That’s also where MGR/I comes in to play, which is basically a measure of compromise between mass, swingweight and balance.

That’s some of the main impacts that swingweight has on the game. I hope this illustrated the essence of swingweight well enough, but I’m always open for questions.